Koord (meetkunde)
'n Koord van 'n kromme is 'n Meetkundige lynsegment waarvan beide die eindpunte op die kromme lê. 'n Snylyn of Sekans is die verlenging van 'n koord.

Koorde van 'n sirkel[wysig | wysig bron]
Van die eieinskappe van koorde van 'n sirkel is as volg:
- Koorde is ewe ver van die middelpunt, as en slegs as hulle lengtes gelyk is.
- 'n Koord se loodregte middellyn gaan deur die middelpunt van die sirkel.
- As die lyn verlengings (sekanslyne) van koorde AB en CD by punt P sny, dan is hulle lengtes AP·PB = CP·PD bevredig (mag van 'n punt teorema).
koorde in trigonometrie[wysig | wysig bron]
Koorde is ekstensief gebruik in die vroeë ontwikkeling van trigonometrie. Die eerste bekende trigonometriese tabel, saamgestel deur Hipparchos, het die waardes van Koordfunksies vir elke 7.5 grade uitgewerk.
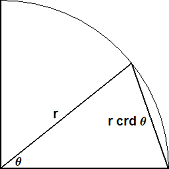
Die koordfunksie word meetkundig deur die figuur na links gedefinieer. Die koord van 'n hoek is die lengte van die koord tussen twee punte op 'n eenheidsirkel verdeel deur daardie hoek. Deur een van die hoeke as nul te neem, kan dit maklik in verband gebring word met die moderne sinus funksie:
Die laaste stap gebruik die halwe-hoek formule. Net soos moderne trigonometrie geskoei is op die sinusfunksie, was antieke trigonometrie geskoei op die koordfunksie. Hipparchos het glo twaalf volumes werk oor koorde geskryf. Die koordfunksie bevredig baie identiteite analoog aan die modernes:
| Name | Sinus-gebaseer | Koord-gebaseer |
|---|---|---|
| Pythagoras | ||
| Half-hoek |
Die halwe-hoek-identiteit versnel die skep van koordtabelle geweldig. Antieke koordtabelle het tipies 'n groot waarde vir die radius van die sirkel gebruik, en die koorde vir die sirkel opgeskryf. Dit is dan 'n eenvoudige saak om te skaleer na om die koord vir 'n eenheidsirkel te bepaal. Volgens G. J. Toomer het Hipparchus 'n sirekel met radius 3438' (=3438/60=57.3) gebruik. Die waarde is geweldig naby die waarde van (=57.29577951...). Een voordeel van die keuse vir die radius is dat hy die benaderde koord van 'n klein hoek baie akkuraat kon bepaal. In moderne terme het dit 'n eenvoudige lineêre benadering moontlik gemaak:
Eksterne skakels[wysig | wysig bron]
- History of Trigonometry Outline
- Trigonometric functions Geargiveer 10 Maart 2017 op Wayback Machine, wat op geskiedenis fokus
- Chord (of a circle) Met interaktiewe animasie







