Traagheidsmoment


Traagheidsmoment is die mate waartoe 'n voorwerp traag is om rondom 'n as te versnel, en word dikwels voorgestel deur die letter I.
Volgens Newton se eerste bewegingswet, sal 'n voorwerp in rus bly of teen dieselfde lineêre snelheid beweeg tensy 'n eksterne netto krag daarop uitgeoefen word – die voorwerp se massa bied dus 'n traagheid om te versnel in 'n lineêre rigting. Traagheidsmoment kan gesien word as 'n analoog van hierdie traagheid van massa, maar wel op 'n voorwerp wat roteer. Dus sal 'n voorwerp wat rondom 'n as roteer in rus bly of teen dieselfde hoeksnelheid beweeg tensy 'n eksterne moment (of aksie wat rotasie veroorsaak) daarop inwerk.
In algemene fisika is die definisie van 'n moment 'krag maal afstand',[1] en kan gesien word as enige aksie wat sal veroorsaak dat 'n voorwerp (of deeltjie binne in 'n voorwerp) rondom 'n as wil roteer. Die traagheidsmoment op enige deeltjie van 'n voorwerp is weer die massa van die deeltjie maal met die kwadraat van afstand van die as (of sentroïede) af. Die som van al die deeltjies se traagheidsmomente tel bymekaar om die traagheidsmoment van die totale voorwerp rondom die as te bepaal. Dus:
- .
waarin
- : traagheidsmoment [eenheid kg.m²]
- : massa van deeltjie i [eenheid kg]
- : afstand van deeltjie i vanaf die as [eenheid m]
Hoe verder 'n deeltjie dus van die as van die voorwerp af geleë is, hoe groter sal die bydrae tot die traagheidsmoment wees.
Molekules in die gasfase kan vrylik roteer en hierdie rotasies is gekwantiseer. Oorgange tussen die verskillende rotasietoestande kan deur absorpsie van mikrogolwe waargeneem word en daardeur kan die molekule se traagheidsmomente bepaal word. (Daar is soms meer as een, as die deeltjie 'n vorm met lae simmetrie besit.)
Traagheidsmomente van verskeie liggame[wysig | wysig bron]
| Sketsvoorstelling | Beskrywing | Traagheidsmoment |
|---|---|---|
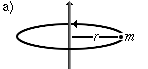
|
'n massapunt op 'n afstand vanaf die draaias. | |
b)
|
'n silinder skil wat om sy silinderas draai. | |
c)
|
'n Soliede silinder wat om sy silinderas draai. | |
d)
|
'n hol silinder wat om sy as draai. | [2] (m: massa van die hol silinder) |

|
'n Vol silinder wat roteer rondom 'n simmetriese as in die middel van sy lengte. | |
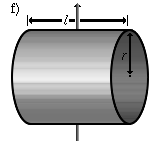
|
'n silinder skil wat roteer rondom 'n simmetriese as in die middel van sy lengte. | |

|
'n Dun staaf wat roteer rondom 'n simmetriese as in die middel van sy lengte. (Let op dat hierdie formule 'n benadering is van die silinder met de aanname dat ) | |
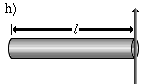
|
'n Dun staaf wat draai rondom een van sy endpunte. | |

|
'n Hol sfeer, met 'n weglaatbare dikte en 'n willekeurige draaias deur die middelpunt. | |
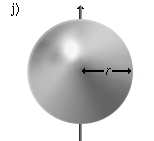
|
'n Soliede sfeer, met 'n willekeurige draaias deur die middelpunt. | |
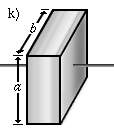
|
'n Plaat met lengtes a en b, met die draaias loodreg op die plaat (vergelyk dun ronde staaf). | |
| Dun skyf, straal r en massa m (gelyk aan soliede silinder). | ||

|
'n Kegel, straal r, hoogte h, en massa m. | |
| Soliede balk, hoogte h, breedte b, diepte d en massa m (vergelyk plaat). |
























