Ellips
'n Ellips is kortliks 'n ovaal: 'n figuur soos ’n sirkel, maar met twee kante wat effens langer en platter is. 'n Lyn wat die verste punte verbind, word die groot, hoof- of lengteas genoem. 'n Lyn wat die naaste punte verbind, word die klein, kort- of breedteas genoem.
In wiskunde is 'n ellips die lokus van punte op 'n vlak waar die some van die afstande van enige punt op die kromme na twee vaste punte konstant is. Die twee vaste punte word die brandpunte genoem.
As 'n keëloppervlak deur 'n vlak gesny word en nie deur die keël se basis gaan nie, is die snyding tussen die keël en die vlak 'n ellips. 'n Eenvoudige bewys dat die bogenoemde twee beskrywings ekwivalent aan mekaar is, kan met Dandelinsfere gedoen word.
Algebraïes is 'n ellips 'n kromme in die Cartesiese vlak gedefinieer deur 'n vergelyking met die vorm:
sodat , waar al die koëffisiënte reël is, en waar meer as een oplossing wat dier punt (x, y) op die ellips, bestaan.
'n Ellips kan geteken word met twee spelde, 'n toulus en 'n potlood. Die spelde word by die brandpunt geplaas en die spelde en potlood word deur die lus ingesluit. Die potlood word op die papier geplaas binne die lus sodat die lus styf gespan is. Die lus sal 'n driehoek vorm. As die potlood beweeg word sodat die lus altyd styf bly sal die som van die afstande van die potlood na die spelde konstant bly wat dan die definisie van 'n ellips bevredig.
Die lynsegment wat deur die brandpunte gaan en op die ellips eindig, word die groot, hoof- of lengteas genoem. Die lengteas loop met die langste segment langs wat deur die ellips gaan. Die lyn wat deur die middelpunt (halfpad tussen die brandpunte) teen 'n regte hoek tot die lengteas gaan, word die klein, kort- of breedteas genoem. 'n Halwe lengteas is die helfte van die lengteas: die lynsegment vanaf die middelpunt, deur 'n brandpunt, tot by die rand van die eillips. Net so is die halwe breedteas die helfte van die breedteas.
As die twee brandpunte saamval, is die ellips 'n sirkel – 'n sirkel is dus 'n spesiale geval van 'n ellips, een waar die eksentrisiteit nul is.
'n Ellips met sy middelpunt by die oorsprong kan gesien word as die beeld van die eenheidsirkel onder 'n lineêre afbeelding geassosieer met 'n simmetriese matriks , waar D 'n diagonale matriks is met die eiewaardes van A, wat beide reël en positief is, langs die hoogdiagonaal, en P 'n reële unitêre matriks met die eievektore van A as kolomme. Dan sal die asse van die ellips langs die eievektore van A lê, en die kwadrate van die lengtes van die asse is die omgekeerdes van die eiewaardes.
'n Ellips kan geproduseer word deur die x-koördinate van alle punte op 'n sirkel met 'n konstante te vermenigvuldig sonder om die y-koördinate te verander.
Parameterisering[wysig | wysig bron]
Die grootte van 'n ellips word bepaal deur twee konstantes, gewoonlik aangedui met a en b. Die konstante a is gelyk aan die lengte van die halwe lengteas en die konstante b aan die lengte van die halwe breedteas. As gevolg hiervan is a altyd groter as b (of gelyk aan mekaar in die geval van 'n sirkel).

'n Ellips met sy middelpunt by die oorsprong van 'n x-y-koördinaatstelsel met sy lengteas langs die x-as, word gedefinieer deur die vegelyking vir die elliptiese voorwerp.
Die afleiding van die formule is nogal insiggewend en nie te moeilik nie.
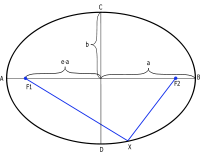
Die volgende diagram vertoon 'n ellips wat die stelling van Pythagoras, a² = b² + c², as 'n spesiale geval van die nieparametriese vergelyking hierbo (x=0, y=b) demonstreer.

Dieselfde ellips word ook beskryf deur die parametriese vergelykings:
wat die trigonometriese funksies sinus en kosinus gebruik.
As 'n ellips se middelpunt nie by die oorsprong van 'n x-y-koördinaatstelsel is nie, maar steeds sy lengteas parallel aan die x-as het, kan dit deur die volgende vergelyking gespesifiseer word
waar (h,k) die middelpunt is.
In poolkoördinate waar die oorsprong een brandpunt van die ellips is, is die vergelyking:
'n Gauss-kaart vorm:
het normaal .
Eksentrisiteit[wysig | wysig bron]
Die vorm van 'n ellips word gewoonlik beskryf deur 'n getal wat die eksentrisiteit van die ellips genoem word, volgens konvensie met e aangedui (dit moet nie met die wiskundige konstante e verwar word nie). Die eksentrisiteit is verwant aan a en b deur die stelling
of waar (die lineêre eksentrisiteit van die ellips) gelyk is aan die afstand van die middelpunt na enige een van die brandpunte
Die eksentrisiteit is 'n positiewe getal minder as 1, of 0 in die geval van 'n sirkel. Hoe groter die eksentrisiteit is, hoe hoër die verhouding van a tot b, en daarom hoe meer uitgerek die ellips. Die ellips in die onderstaande beeld het 'n eksentrisiteit van ongeveer 0.8733. Die afstand tussen die brandpunte is 2ae.
Semi-latus rectum en poolkoördinate[wysig | wysig bron]
Die semi-latus rectum van 'n ellips, gewoonlik aangedui (kleinletter L), is die afstand van 'n brandpunt van die ellips na die ellips self, gemeet langs 'n lyn loodreg tot die hoofas. Dit is verwant aan en (die ellips se halwe asse) deur die formule of, as eksentrisiteit gebruik word, .
Kyk ook[wysig | wysig bron]




















