Heks van Agnesi
| Hierdie artikel is 'n weesbladsy. Dit is nie geskakel of in ander bladsye ingesluit nie. Help Wikipedia deur na moontlike teks te soek en 'n skakel hierheen te plaas. |
In wiskunde, is die heks van Agnesi, soms die heks van Maria Agnesi genoem (vernoem na Maria Agnesi) die kromme wat as volg gedefinieer word.
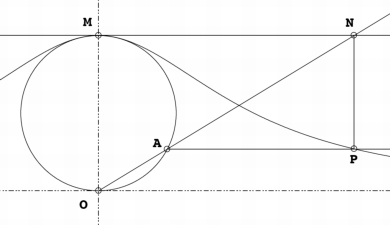
Begin met 'n vaste sirkel, 'n punt O op die sirkel word gekies. Vir enige ander punt A op die sirkel, word die snylyn OA geteken. Die punt M is lynreg oorkant O. Die lyn OA sny die raaklyn M by die punt N. Die lyn parallel aan OM deur N, en die lyn loodreg tot OM deur A sny by P. Soos die punt A gevarieer is die pad wat P volg die heks.
Die kromme is asimptoties tot die raaklyn van die vaste sirekel deur die punt O.
Vergelykings[wysig | wysig bron]
Veronderstel die punt O is die oorsprong, en dat M op die positiewe y-as is. Veronderstel die radius van die sirkel is a.
Dan het die kromme die Cartesiese vergelyking .
Let daarop dat as a=1/2, dan word die vergelyking die baie eenvoudige
Parametries, as is die hoek tussen OM en OA, regsom gemeet, dan word die kromme gegee deur die vergelykings
Voorbeelde[wysig | wysig bron]
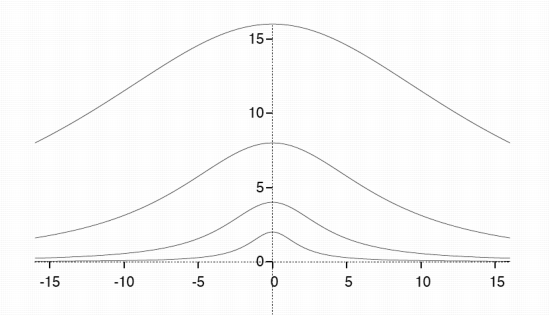
Die figuur na regs wys voorbeelde van die kromme vir a=1, a=2, a=4, en a=8.
Eienskappe[wysig | wysig bron]
- Die oppervlak tussen die Heks en die asimptoot daarvan is vier keer die oppervlak van die oppervlak van die vaste sirkel (d.w.s: ).
- Die omwentelingsvolume van die Heks, om sy asimptoot is .
- Die swaartepunt van die kromme is by .
Geskiedenis[wysig | wysig bron]
Die kromme is in 1701 deur Fermat, Guido Grandi en in 1748 deur Maria Agnesi bestudeer.
In Italiaans word die kromme la versiera di Agnesi genoem wat "die kromme van Agnesi" beteken. Dit is op 'n stadium deur professor John Colson van Cambridge geïnterpreteer as "l'avversiera di Agnesi" waar "avversiera" "heks" beteken en die wanvertaling het behoue gebly.
Eksterne skakels[wysig | wysig bron]
- Engines of Our Ingenuity. Episode No. 217: The Witch of Agnesi deur John H. Lienhard
- Weisstein, Eric W., Witch of Agnesi op MathWorld.







