Vektor (Wiskunde)
In wiskunde, fisika en ingenieurswese, is 'n vektor 'n meetkundige voorwerp wat 'n lengte en 'n rigting het. Formeel word 'n vektor gedefinieer as 'n element van 'n vektorruimte. Een van die algemeenste vektore is die driedimensionele vektor, wat 'n punt in driedimensionele ruimte beskryf. So 'n punt kan voorgestel word deur sy drie koördinate: x, y en z. Die vektor kan dan as 'n pyl gesien word, wat by die oorsprong - die punt met koördinate (0,0,0) - begin en by die punt (x,y,z) eindig. Sulke pyle word gebruik om eienskappe soos snelheid, verplasing, versnelling en krag te beskryf. Die term vektor is in 1837 ingevoer deur William Rowan Hamilton, en is aanvanklik gebruik om slegs driedimensionele vektore te beskryf. Die term word deesdae in 'n baie breër sin gebruik, aangesien daar geweldig baie verskillende vektorruimtes bestaan.
Voorstelling van 'n vektor
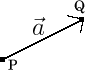
[wysig | wysig bron]Om vektore van skalare te onderskei, word vektore gewoonlik in vetdruk uitgebeeld, soos a, of as 'n letter met 'n pyltjie bo-op, soos , of as 'n hoofletter A. Dit is egter slegs notasie, en daar bestaan baie uitsonderings hierop. Die lengte, of grootte van die vektor word aagedui soos volg: . 'n Vektor kan as 'n pyltjie voorgestel word:
Die vektor a word dan ook geskryf as . Twee vektore is gelyk aan mekaar, as hulle dieselfde grootte en rigting het. As die beginspunt van die vektor belangrik is, dan word dit 'n gebonde vektor genoem. Maar as die beginspunt nie belangrik is nie, dan is die volgende twee vektore gelyk aan mekaar:
Vektorbasis
[wysig | wysig bron]'n Belangrike konsep is die van 'n vektorbasis. 'n Basis is 'n stel vektore wat gerek en bymekaargetel kan word om enige ander vektor te gee. Byvoorbeeld, in drie dimensies vorm die eenheidsvektor in die x rigting (dit is 'n vektor, aangedui deur ex, wat direk in die x rigting wys en 'n lengte van 1 het), die eenheidsvektor in die y rigting (ey), en die eenheidvektor in die z rigting (ez) 'n basis. Enige driedimensionele vektor kan beskryf word deur 'n sekere afstand in die x rigting te gaan, en dan 'n afstand in die y rigting, en dan 'n afstand in die z rigting. Wiskundig gesproke skryf ons:
Waar ax die lengte van die vektor in die x rigting is, ay die lengte in die y rigting, en az die lengte in die z rigting. Ander, maar gelykstaande formate is om die vektor in sy ryvorm, (ax, ay, az) of in sy kolomvorm te skryf:
Soms word daar ook van 'n basis gebruikgemaak wat nie mooi in die x, y , en z rigtings wys nie. Die basisvektors word dan gewoonlik as die versameling vektors {e1, e2, e3} geskryf, en die vektor a kan dan in terme van hierdie basis geskryf word as:
Waar a1 die lengte van die vektor in die e1 rigting is, en soortgelyk vir die ander rigtings.
Bronne
[wysig | wysig bron]| Wikimedia Commons bevat media in verband met Vector mathematics. |
- Die Nederlandse en Engelse Wikipedias het materiaal tot hierdie artikel bygedra.