Elementêre wiskunde

'n Versameling van meetkundige vorms. Alle vorms van 'n gegewe kleur is soortgelyk aan mekaar. Vorms en basiese meetkunde is belangrike onderwerpe in elementêre wiskunde

'n Illustrasie wat appels gebruik om aan te dui dat 2 + 3 en 3 + 2 albei gelyk is aan 5. Appels word gereeld gebruik om rekenkunde in handboeke vir kinders te verduidelik.

Elementêre wiskunde bestaan uit wiskunde-onderwerpe wat dikwels op primêre of sekondêre skoolvlak aangebied word.

Die mees basiese onderwerpe in elementêre wiskunde is rekenkunde en meetkunde. Sedert die laaste dekades van die 20ste eeu, is daar meer klem gelê op probleemoplossing. Elementêre wiskunde word in die alledaagse lewe gebruik in sulke aktiwiteite soos verandering, kook, koop en verkoop van voorraad, en dobbel. Dit is ook 'n noodsaaklike eerste stap op die pad na die verstaan van die wetenskap.

Op sekondêre skool is die hoofonderwerpe van elementêre wiskunde algebra en trigonometrie. Calculus, hoewel dit dikwels aan gevorderde sekondêre skoolstudente geleer word, word gewoonlik as kollege-vlak wiskunde beskou.

Onderwerpe

Volgens 'n oorsig van die wiskundekurrikulum van lande wat aan die TIMSS-eksamen deelgeneem het, is die volgende onderwerpe belangrik vir die elementêre kurrikulum (jare 1-8) deur minstens twee derdes van die hoogspresterende lande:

Heelgetalle

Die heelgetalle is dié wat gebruik word om te tel (soos in "daar is ses munte op die tafel") en te orden (soos in "hierdie is die derde grootste stad in die land"). In algemene taal word hierdie doeleindes onderskei deur onderskeidelik kardinale en ordinale getalle te gebruik. 'n Derde gebruik van natuurlike getalle is as nominale getalle, soos die modelnommer van 'n produk, waar die natuurlike getal slegs gebruik word vir die benaming (afgesien van 'n reeksnommer waar die volgorde eienskappe van die natuurlike getalle later gebruike onderskei van vorige gebruike).

Eienskappe van die natuurlike getalle soos verdeelbaarheid en die verspreiding van priemgetalle, word bestudeer in basiese getalteorie, 'n ander deel van elementêre wiskunde.

Elementêre wiskunde fokus op die (+) en (×) bewerkings en hul eienskappe:

Sluiting onder toevoeging en vermenigvuldiging: vir alle natuurlike getalle a en b, beide a + b en a × b is natuurlike getalle.

 Assosiativiteit: vir alle natuurlike getalle a, b en c, a + (b + c) = (a + b) + c en a × (b × c) = (a × b) × c. Kommutativiteit: vir alle natuurlike getalle a en b, a + b = b + a en a × b = b × a.

 Bestaande identiteitselemente: vir elke natuurlike getal a, a + 0 = a en a × 1 = a.

 Verdelingsvermoë van vermenigvuldiging oor optelling vir alle natuurlike getalle a, b en c, a × (b + c) = (a × b) + (a × c).

 Geen nie-nul-verdelers: as a en b natuurlike getalle is, is a × b = 0, dan a = 0 of b = 0.

Meeteenhede

'n Meeteenheid is 'n definitiewe grootte van 'n fisiese hoeveelheid, gedefinieer en aangeneem deur konvensie of wetgewing, wat gebruik word as 'n standaard vir die meting van dieselfde fisiese hoeveelheid. Enige ander waarde van die fisiese hoeveelheid kan uitgedruk word as 'n eenvoudige veelvoud van die meeteenheid. Byvoorbeeld, lengte is 'n fisiese hoeveelheid. Die meter is 'n lengte-eenheid wat 'n definitiewe voorafbepaalde lengte verteenwoordig. Wanneer ons 10 meter (of 10 m) sê, beteken ons eintlik 10 keer die bepaalde voorafbepaalde lengte wat "meter" genoem word.

Die definisie, ooreenkoms en praktiese gebruik van meeteenhede het 'n deurslaggewende rol gespeel in die menslike strewe vanaf die vroeë eeue tot op hierdie dag. Verskillende stelsels eenhede was baie algemeen. Nou is daar 'n globale standaard, die Internasionale Stelsel van Eenhede (SI), die moderne vorm van die metrieke stelsel.

Breuke

'n Breuk verteenwoordig 'n deel van 'n geheel of meer algemeen 'n aantal gelyke dele. Wanneer dit in die alledaagse Engels gepraat word, beskryf 'n breuk hoeveel dele van 'n bepaalde grootte daar byvoorbeeld is, 'n halwe, agt vyfde, driekwart. 'n Algemene, vulgêre of eenvoudige breuk (voorbeelde: ${\tfrac {1}{2}}$ en ${\tfrac {17}{3}}$) bestaan uit 'n heelgetal teller wat bokant 'n lyn vertoon word (of voor 'n snit) en 'n nie- , hieronder (of na) daardie lyn vertoon. Getalle en noemers word ook gebruik in breuke wat nie algemeen is nie, insluitend saamgestelde breuke, komplekse breuke en gemengde syfers.

Soos heelgetalle, volg breuke die kommutatiewe, assosiatiewe en verspreidende wette, en die reël teen verdeling met nul.

Vergelykings en formules

'n Formule is 'n entiteit wat gebruik word deur die simbole en formasie reëls van 'n gegewe logiese taal te gebruik. Byvoorbeeld, die bepaling van die volume van 'n sfeer vereis 'n beduidende hoeveelheid integraalrekene of sy meetkundige analoog, die metode van uitputting; Maar nadat hierdie een keer gedoen is in terme van 'n parameter (die radius byvoorbeeld), het wiskundiges 'n formule gemaak om die volume te beskryf. 'n Vergelyking is 'n formule van die vorm A = B, waar A en B uitdrukkings is wat een of meer veranderlikes insluit wat onbekende genoem word, en "=" dui die gelykwaardige binêre verband aan. Alhoewel dit in die vorm van 'n voorstel geskryf word, is 'n vergelyking nie 'n stelling wat waar of onwaar is nie, maar 'n probleem wat bestaan uit die vind van die waardes, genoem oplossings, wat, wanneer die onbekende vervang word, gelyke waardes van die uitdrukkings A en B lewer. Byvoorbeeld, 2 is die unieke oplossing van die vergelyking x + 2 = 4, waarin die onbekende x is.

Data-voorstelling en analise

'n Histogram-voorbeeld van die hoogtes van 31 Swart Kersiebome. Histogramme is 'n algemene instrument wat gebruik word om data te verteenwoordig.

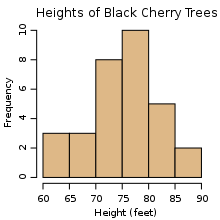
Data is 'n stel waardes van kwalitatiewe of kwantitatiewe veranderlikes; hersaamgestel, stukkies data is individuele stukke inligting. Data in rekenaarwese (of dataverwerking) word voorgestel in 'n struktuur wat dikwels tabulêr is (verteenwoordig deur rye en kolomme), 'n boom ('n stel nodusse met ouer-kinders-verhouding) of 'n grafiek ('n stel verbind nodes). Data is tipies die gevolg van metings en kan met behulp van grafieke of beelde gevisualiseer word.

Data as 'n abstrakte konsep wat kan beskou word as die laagste vlak van abstraksie, van watter inligting en dan kennis afgelei word.

Basiese twee-dimensionele meetkunde

Tweedimensionele meetkunde is 'n tak van wiskunde wat verband hou met vrae van vorm, grootte en relatiewe posisie van tweedimensionele figure. Basiese onderwerpe in elementêre wiskunde sluit veelhoeke, sirkels, omtrek en area in.

'n Poligoon wat begrens word deur 'n eindige ketting van reguitlynsegmente wat in 'n lus gesluit word om 'n geslote ketting of kring te vorm. Hierdie segmente heet sy kante of sye, en die punte waar twee kante ontmoet, is die veelhoek se hoekpunte (enkelvoud: hoekpunt) of hoeke. Die binnekant van die veelhoek word soms sy liggaam genoem. 'N N-gon is 'n veelhoek met n sye. 'N Veelhoek is 'n 2-dimensionele voorbeeld van die meer algemene politoop in enige aantal dimensies.

'n Sirkel is 'n eenvoudige vorm van tweedimensionele meetkunde wat die stel van alle punte in 'n vliegtuig is wat op 'n gegewe afstand van 'n gegewe punt, die middelpunt is. Die afstand tussen enige van die punte en die middel word die radius genoem. Dit kan ook gedefinieer word as die lokus van 'n punt wat ewe ver van 'n vaste punt af is.

'n Sirkel is 'n eenvoudige vorm van tweedimensionele geometrie wat die stel van alle punte in 'n vliegtuig is op 'n gegewe afstand van 'n gegewe punt, die middelpunt is. Die afstand tussen enige van die punte en die middel word die radius genoem. Dit kan ook gedefinieer word as die lokus van 'n punt wat ewe ver van 'n vaste punt af is.

Oppervlakte is die hoeveelheid wat die omvang van 'n tweedimensionele figuur of vorm uitdruk. Daar is verskeie bekende formules vir die areas van eenvoudige vorms soos driehoeke, reghoeke en sirkels.

Afronding en beduidende syfers

Om 'n numeriese waarde af te rond, beteken om dit te vervang deur 'n ander waarde wat ongeveer gelyk is, maar 'n korter, eenvoudiger of meer eksplisiete voorstelling het. Byvoorbeeld, kan £ 23.4476 vervang word met £ 23.45, of die breuk 312/937 met 1/3, of die uitdrukking √2 met 1.414. Afronding word dikwels doelbewus gedoen om 'n waarde te kry wat makliker is om te skryf en te hanteer as die oorspronklike. Dit kan ook gedoen word om die akkuraatheid van 'n berekende nommer aan te dui; byvoorbeeld, 'n hoeveelheid wat bereken is as 123 456, maar bekend is dat dit slegs binne enkele honderde eenhede akkuraat is, word eerder as "ongeveer 123 500" vermeld.

The significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except:

• Alle voorste nulle; Nulpunte wanneer hulle bloot plekhouers is om die skaal van die nommer aan te dui (presiese reëls word verduidelik by die identifisering van beduidende syfers); en Spuwende syfers, byvoorbeeld, deur berekeninge uitgevoer na groter akkuraatheid as die oorspronklike data, of metings wat meer akkuraat gerapporteer word as wat die toerusting ondersteun.

Skatting

Skatting is die proses om 'n skatting of benaderings te vind, wat 'n waarde is wat vir een of ander doel bruikbaar is, selfs al is insetdata dalk onvolledig, onseker of onstabiel. Die waarde is egter bruikbaar omdat dit afgelei is van die beste beskikbare inligting..

'n Informele skatting wanneer min inligting beskikbaar is, word 'n guesstimate genoem, omdat die ondersoek nader kom as om die antwoord net te raai.

Desimale

'n Desimale breuk is 'n breuk waarvan die noemer 'n krag van tien is.

Desimale breuke word algemeen uitgespreek sonder 'n noemer, die desimale skeier word in die teller ingevoeg (met die toonaangewende nulpunte bygevoeg indien nodig) in die posisie regs wat ooreenstem met die krag van tien van die noemer; Bv. 8/10, 83/100, 83/1000 en 8/10000 word uitgedruk as 0.8, 0.83, 0.083 en 0.0008. In Engelssprekende lande, sommige Latyns-Amerikaanse en baie Asiatiese lande, word 'n periode (.) of verhoogde periode (·) as die desimale skeidingsteken gebruik; In baie ander lande, veral in Europa, word 'n komma (,) gebruik.

Persentasies

'n Persentasie is 'n getal of verhouding uitgedruk as 'n fraksie van 100. Dit word dikwels aangedui met die persentteken, %, of die afkorting "pct." 'n Persentasie is 'n dimensielose nommer (suiwer getal).

Byvoorbeeld, 45% (lees as "vyf-en-veertig persent") is gelyk aan 45/100, of 0.45. Persentasies word gebruik om uit te druk hoe groot of klein een hoeveelheid relatief tot 'n ander hoeveelheid is. Die eerste hoeveelheid verteenwoordig gewoonlik 'n deel van, of 'n verandering in, die tweede hoeveelheid. Byvoorbeeld, 'n toename van $ 0.15 teen 'n prys van $ 2.50 is 'n toename met 'n breuk van 0.15 / 2.50 = 0.06. Uitgedruk as 'n persentasie, is dit dus 'n 6% -verhoging. Terwyl persentasie waardes dikwels tussen 0 en 100 is, is daar geen beperking nie en kan 'n mens byvoorbeeld na 111% of -35% verwys.

Verhoudings

Twee hoeveelhede is proporsioneel as 'n verandering in een altyd vergesel is van 'n verandering in die ander, en as die veranderinge altyd verwant is aan die hand van 'n konstante vermenigvuldiger. Die konstante word die koëffisiënt van eweredigheid of eweredigheidskonstante genoem.

• As een hoeveelheid altyd die produk van die ander is en 'n konstante, word die twee regstreeks proporsioneel. X en y is direk eweredig as die verhouding ${\tfrac {y}{x}}$ konstant is.
•  As die produk van die twee hoeveelhede altyd gelyk is aan 'n konstante, word die twee gesê om omgekeerd eweredig te wees. X en y is omgekeerd eweredig as die produk xy konstant is.

Analitiese meetkunde

Cartesiese koördinate

Analitiese meetkunde is die studie van meetkunde met behulp van 'n koördinaatstelsel. Dit kontrasteer met sintetiese geometrie.

Gewoonlik word die Cartesiese koördinaatstelsel gebruik om vergelykings vir vliegtuie, reguit lyne en vierkante te manipuleer, dikwels in twee en soms in drie dimensies. Geometries ondersoek mens die Euklidiese vlak (2 dimensies) en Euklidiese ruimte (3 dimensies). Soos in skoolboeke geleer, kan analitiese meetkunde eenvoudiger verklaar word: dit is om numeriese meetkundige vorms op numeriese wyse te omskryf en numeriese inligting uit vorms se numeriese definisies en voorstellings te onttrek.

Transformasies is maniere om funksies te verskuif en te skaal deur verskillende algebraïese formules te gebruik.

Negatiewe getalle

'n Negatiewe getal is 'n reële getal wat minder as nul is. Sulke getalle word dikwels gebruik om die bedrag van 'n verlies of afwesigheid te verteenwoordig. Byvoorbeeld, 'n skuld wat verskuldig is, kan as 'n negatiewe bate beskou word, of 'n afname in sommige hoeveelheid kan as 'n negatiewe toename beskou word. Negatiewe getalle word gebruik om waardes te beskryf op 'n skaal wat onder nul val, soos die Celsius- en Fahrenheit-skale vir temperatuur.

Eksponente en radikale

Eksponisasie is 'n wiskundige operasie, geskryf as bn, wat twee getalle, die basis b en die eksponent (of krag) n insluit. Wanneer n 'n natuurlike getal is (dws 'n positiewe heelgetal), stem die eksponensiëring ooreen met herhaalde vermenigvuldiging van die basis: dit is, bn is die produk van die vermenigvuldiging van n basisse:

$b^{n}=\underbrace {b\times \cdots \times b} _{n}$

Wortels is die teenoorgestelde van eksponente. Die nde wortel van 'n getal x (geskryf ${\sqrt[{n}]{x}}$) is 'n getal r, wat wanneer dit verhoog word na die mag n, x lewer. Dit is,

${\sqrt[{n}]{x}}=r\iff r^{n}=x,$

Waar n die graad van die wortel is. 'n Wortel van graad 2 word 'n vierkantswortel genoem en 'n wortel van graad 3, 'n kubuswortel. Wortels van hoër graad word verwys deur die gebruik van ordinale getalle, soos in vierde wortel, twintigste wortel, ens.

Byvoorbeeld:

• 2 is 'n vierkant wortel van 4, sedert 2² = 4.
• -2 is ook 'n vierkant wortel van 4, aangesien (-2)² = 4.

Kompas-en-liniaal

Kompas-en-reguit, ook bekend as liniaal-en-kompas konstruksie, is die konstruksie van lengtes, hoeke en ander meetkundige figure met slegs 'n geïdealiseerde liniaal en kompas.

Die geïdealiseerde liniaal, bekend as 'n reguitlyn, word aangeneem as oneindig in lengte en het geen merke daarop nie en slegs een rand. Die kompas word veronderstel om ineen te val wanneer dit van die bladsy opgehef word, dus mag dit nie direk gebruik word om afstande oor te dra nie. (Dit is 'n onbelangrike beperking, aangesien 'n afstand met behulp van 'n meervoudige prosedure gebruik kan word, selfs met 'n ineenstortende kompas, sien kompas-ekwivalentstelling.) Meer formeel, die enigste toelaatbare konstruksies is dié wat deur Euclid se eerste drie postulate verkry word.

Kongruensie en gelykvormigheid

Twee figure of voorwerpe is kongruent as hulle dieselfde vorm en grootte het, of as een dieselfde vorm en grootte het as die spieëlbeeld van die ander. Meer formeel word twee stelle punte kongruent genoem, en slegs as 'n mens deur 'n isometrie omskep kan word, dws 'n kombinasie van rigiede bewegings, naamlik 'n vertaling, 'n rotasie en 'n refleksie. Dit beteken dat enige voorwerp kan herposisioneer en weerspieël word (maar nie verander nie) sodat dit presies met die ander voorwerp saamval. So twee duidelike vliegtuigfigure op 'n stuk papier is kongruent as ons hulle kan uitsny en hulle dan heeltemal ooreenstem. Om die papier oor te laat is toegelaat.

Twee meetkundige voorwerpe word dieselfde genoem as hulle albei dieselfde vorm het, of een het dieselfde vorm as die spieëlbeeld van die ander. Meer presies kan mens van die ander verkry word deur eenvormig te skaal (vergroot of krimp), moontlik met addisionele vertaling, rotasie en refleksie. Dit beteken dat enige voorwerp kan herroep, herposisioneer en weerspieël word, sodat dit presies met die ander voorwerp saamval. As twee voorwerpe soortgelyk is, is elkeen kongruent tot die resultaat van 'n eenvormige skaal van die ander.

Drie-dimensionele meetkunde

Vaste meetkunde was die tradisionele naam vir die geometrie van driedimensionele Euklidiese ruimte. Stereometrie handel oor die metings van volumes van verskillende soliede figure (driedimensionele figure), insluitende piramides, silinders, keëls, afgeknotte keëls, sfere en prismas.

Rasionele getalle

Rasionale getal is enige getal wat uitgedruk kan word as die kwosiënt of breuk p / q van twee heelgetalle, met die noemer q nie gelyk aan nul nie. Aangesien q gelyk is aan 1, is elke heelgetal 'n rasionale getal. Die stel van alle rasionale getalle word gewoonlik aangedui deur 'n vetgrens Q (of swartbordvoetbal \ mathbb {Q}).

Patrone, verhoudings en funksies

'n Patroon is 'n waarneembare reëlmatigheid in die wêreld of in 'n mensgemaakte ontwerp. As sodanig herhaal die elemente van 'n patroon op 'n voorspelbare wyse. 'n Meetkundige patroon is 'n soort patroon wat gevorm word van meetkundige vorms en tipies herhaal soos 'n plakpapier.

'n Verhouding op 'n stel A is 'n versameling bestelde pare elemente van A. Met ander woorde, dit is 'n deelversameling van die Cartesiese produk A2 = A × A. Algemene verhoudings sluit in verdeelbaarheid tussen twee getalle en ongelykhede.

'n Funksie is 'n verband tussen 'n stel insette en 'n stel toelaatbare uitsette met die eienskap dat elke inset verband hou met presies een uitset. 'n Voorbeeld is die funksie wat elke reële getal x verband hou met sy vierkant x2. Die uitset van 'n funksie f wat ooreenstem met 'n inset x word aangedui deur f (x) (lees "f of x"). In hierdie voorbeeld, as die inset -3 is, is die uitset 9, en ons kan f (-3) = 9 skryf. Die insetveranderlike (s) word soms die argument (e) van die funksie genoem.

Hellings en trigonometrie

Die helling van 'n lyn is 'n getal wat beide die rigting en die steilheid van die lyn beskryf. Helling word dikwels aangedui met die letter m..

Trigonometrie is 'n tak van wiskunde wat verhoudings met lengtes en hoeke van driehoeke bestudeer. Die veld het gedurende die 3de eeu vC voorgekom van toepassings van meetkunde tot astronomiese studies..

Verenigde State Van Amerika

In die Verenigde State was daar baie kommer oor die lae vlak van elementêre wiskundevaardighede van baie studente, in vergelyking met studente in ander ontwikkelde lande. Die No Child Left Behind-program was een poging om hierdie tekort aan te spreek, wat vereis dat alle Amerikaanse studente in elementêre wiskunde getoets word.