Pythagoras se stelling

Pythagoras se Stelling is 'n wiskundige stelling wat vernoem is na die Griekse wiskundige, Pythagoras. Volgens tradisie het Pythagoras die stelling ontdek en bewys,[1] maar die stelling se resultaat was voor Pythagoras se ontdekking aan verskeie antieke bevolkings bekend, waaronder die Egiptenare en die Indiërs.
Die stelling is as volg:
In enige reghoekige driehoek is die kwadraat van die lengte van die skuinssy gelyk aan die som van die kwadrate van die lengtes van die reghoekige sye.
Dit wil sê, gestel daar is 'n reghoekige driehoek met 'n skuinssy met 'n lengte van c en twee reghoekige sye met die lengtes a en b, dan kan die stelling in as die volgende vergelyking uitgedruk word:
Of, om c op te los:
Hierdie vergelyking bied 'n maklike manier om die onbekende lengte van 'n sy van 'n reghoekige driehoek uit te werk, mits die ander twee reeds bekend is.
Bewys met gelykvormige driehoeke
[wysig | wysig bron]
Van die beeld . En deur die vervanging van vergelykings (1) en (2):
Vermenigvuldig vir c:
Multidimensionele meetkunde
[wysig | wysig bron]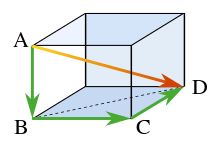
Pythagoras se stelling kan uitgebrei word na multidimensionele meetkunde. As 'n driedimensionele voorbeeld, kyk na die diagram aan die regterkant. Volgens Pythagoras se stelling is die lengte van diagonale 'BD' deur:
gegee hierdie drie kante 'n regte driehoek vorm. Die horisontale diagonale BD en die vertikale rand AB vorm 'n tweede reghoekige driehoek met AD as sy diagonaal. Volgens Pythagoras se stelling is die lengte van diagonale AD deur:
gegee.
As dit as 'n enkele stap gedoen word, dan
Hierdie resultaat is die driedimensionele uitdrukking vir die grootte van 'n vektor v (die diagonale AD) in terme van sy ortogonale komponente {vk} ( die drie wedersydse loodregte kante):
Hierdie proses kan uitgebrei word na arbitrêre aantal dimensies.
Verwysings
[wysig | wysig bron]- ↑ Heath, Sir Thomas. A History of Greek Mathematics (2 Vols.), Clarendon Press, Oxford (1921), Dover Publications, Inc. (1981), ISBN 0-486-24073-8. Vol 1, bl, 144.











