Kristalstruktuur

Baie vaste stowwe het 'n kristallyne struktuur. Dit wil sê dat hulle bestaan uit 'n reëlmatige stapeling van 'n strukturele eenheid (molekules, ione, atome) wat as boustene daarvan beskou kan word. Die strukturele eenhede vorm 'n driedimensionale rooster. In kristallografie word die gestapelde strukturele eenhede eenheidselle genoem.
Die reëlmatige stapeling word (Parallelle) verskuiwingsimmetrie genoem. Naas die verskuiwingsimmetrie bestaan daar ook die interne simmetrie binne dié eenhede. Die somtotaal van die soorte simmetrieë word die kristalstruktuursimmetrie genoem.
'n Tegniek wat gebruik kan word om die kristalstruktuur te bepaal is X-straaldiffraksie. Dit is tot op hede (2003) nog die noukeurigste metode om die struktuur van molekules en van nie-molekulêre roosters te ondersoek. Die kristalstrukture van meer as 250 000 organiese verbindings is reeds bepaal en opgeteken in die Cambridge Structural Database. Die golflengte van X-strale het dieselfde grootteorde as die eenheidselle, ongeveer 1 nm. 'n Ander diffraksietegniek wat dit vermag is neutrondiffraksie.
Buiten kristallyne vaste stowwe bestaan daar ook glasstrukture en amorfe strukture.
Kristalsimmetrie[wysig | wysig bron]
Kristalstrukture word gekenmerk deur hul simmetrie. Daar kan tussen twee vorme van simmetrie onderskei word:
- verskuiwingsimmetrie tussen die eenheidselle
- interne simmetrie tussen verskillende dele van die eenheidsel
Verskuiwingsimmetrie[wysig | wysig bron]
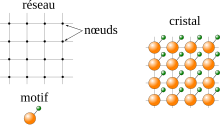
Verskuiwingsimmetrie beteken dat 'n mens die struktuureenheid telkens opnuut teëkom wanneer 'n mens 'n bietjie verder af (die blik verskuif) in die kristal kyk. Hierdie verskuiwingsimmetrie kan op sy beste beskryf word deur 'n eenheidsvektor. Omdat 'n kristal driedimensionaal is word daar vir 'n volledige beskrywing, drie sulke vektore of selasse benodig wat nié in een vlak lê nie.
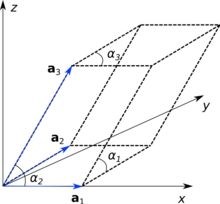
Gesamentlik vorm hierdie vektore 'n parallellopipedum of blok wat die eenheidsel genoem word. Die drie eenheidsvektore (a,b,c) word die selasse of selkonstantes genoem. Verskuiwingsimmetrie kan beskryf word as 'n Abeliese groep. Die elemente kan geskryf word as {E|000}, {E|100}, {E|010} of {E|101} ensomeer waar die getal ná die identiteitselement E aangee wat die verskuiwingsvektor aangee. Die groep is Abelies omdat twee elemente altyd kommuteer: hulle volgorde maak nie saak nie: {E|011}{E|110}={E|110}{E|011}={E|121}
Bravais-tralies[wysig | wysig bron]
Kristalle het gewoonlik meer as net verskuiwingsimmetrie, daar is dikwels ook rotasiesimmetrie, met elemente soos tweetallige asse wat met {C2|000} aangedui kan word of kombinasies soos {C2|100}. (Lees: roteer oor 180° en skuif een eenheidsvektor in die a-rigting) Hierdie elemente vorm 'n ruimtegroep, wat gewoonlik nie Abelies meer is nie.
Afhangende van die aan- of afwesigheid van rotasiesimmetrie kan die asse willekeurige hoeke (α,β,γ) met mekaar vorm of moet hulle haaks ten opsigte van mekaar staan. Daar word ook aan die relatiewe lengtes van hierdie asse, afhangende van die oorhoofse simmetrie, beperkinge opgelê. Die volgende is moontlike roosters:
- triklinies (a, b, c, α, β, γ almal willekeurig)
- monoklinies (a, b, c, β almal willekeurig, α = γ = 90°)
- ortorombies (a, b, c willekeurig, α = β = γ = 90°)
- tetragonaal (a = b, c willekeurig, α = β = γ = 90°)
- romboëdries (a = b = c, α = β = γ)
- heksagonaal (a = b, c willekeurig, α = β = 90° γ = 120°)
- kubies (a = b = c, α = β = γ = 90°)
'n Konvensie wat in kristallografie gevolg word is dat daar sover moontlik gepoog word om van die hoogste moontlike simmetrie gebruik te maak om 'n kristalrooster te beskryf. Verder word daar ook waar moontlik die kortste asse a, b en c gebruik wat die rooster korrek kan beskryf.
In sommige gevalle is dit moontlik om 'n rooster te beskryf met 'n hoër simmetrie deur die volume van die eenheidsel met 2, 3 of 4 te vermenigvuldig (sentrering). Dit lei dan tot 'n sogenaamde nie-primitiewe rooster. Daar is 14 kombinasies van roosters met sentrering, die sogenaamde Bravais-tralies.
Interne simmetrie[wysig | wysig bron]
Die interne simmetrie tussen verskillende dele van die eenheidsel kan die vorm aanneem van 'n inversie (die omkeer van al drie die ruimtekoördinate), 'n spieëling (die loodregte omkeer van 'n ruimtekoördinaat ten opsigte van 'n denkbeeldige vlak) en 'n rotasie (die draai van die ruimte om 'n denkbeeldige lyn). Omdat 'n kristalstruktuur altyd ook 'n verskuiwingsimmetrie het, kom slegs 2-, 3-, 4- of 6-voudige rotasiesimmetrie voor. Naas suiwer spieëling en rotasie is daar ook kombinasies van spieëling en rotasie moontlik met klein verskuiwings (kleiner as die verskuiwing tussen eenheidselle).
Kristalstrukture in die verskillende roostersoorte kan verskillende simmetrie-elemente bevat:
- 'n Trikliniese kristalstruktuur kan slegs inversiesimmetrie bevat
- 'n Monokliniese kristalstruktuur het 'n dubbele rotasie of 'n dubbele rotasie en 'n spieëling of 'n kombinasie van die twee.
- 'n Ortorombiese struktuur het drie dubbele rotasies of twee dubbele rotasies en 'n spieëling of drie spieëlings.
- 'n Tetragonale struktuur het ten minste een viervoudige rotasie
- 'n Romboëdriese of 'n heksagonale struktuur het ten minste een drievoudige rotasie
- 'n Kubiese struktuur het ten minste een drievoudige rotasie (langs die liggaamsdiagonaal van die kubus) en drie twee- of viervoudige rotasies langs die drie asse en/of drie spieëlvlakke loodreg ten opsigte van die asse.
Alle moontlike kombinasies van roostersoorte met alle kombinasies van interne simmetrie wat daarin kan voorkom lewer presies 230 ruimtegroepe.
Klassifikasie van roosters[wysig | wysig bron]
Die roosters kan op verskeie maniere ingedeel word. Daar is in totaal sewe kristallografiese stelsels, wat in 14 sogenaamde Bravaistralies verdeel kan word. Hierdie tralies en stelsels word in die onderstaande tabel weergegee.
| triklinies | primitief | |||

|
||||
| monoklinies | primitief | grondvlak- gesentreerd |
||

|

|
|||
| ortorombies | primitief | grondvlak- gesentreerd |
ruimtelik- gesentreerd |
vlak- gesentreerd |

|

|

|

| |
| heksagonaal | primitief | |||

| ||||
| romboëdries (trigonaal) |
primitief | |||

| ||||
| tetragonaal | primitief | ruimtelik- gesentreerd |
||

|

|
|||
| kubies (isometries) |
primitief | ruimtelik- gesentreerd |
vlak- gesentreerd | |

|

|

|
