Driehoek

Die som van die hoeke is 180°

'n Driehoek is 'n veelhoek wat uit drie sye en drie hoeke bestaan. 'n Kenmerk van die enige driehoek wat in 'n Euklidiese tweedimensionele ruimte lê ('n vlak driehoek) is dat die som van hoeke altyd 180 °grade is, maar die som van die hoeke van 'n sferiese driehoek is altyd meer dan 180°.

By 'n reghoekige driehoek is die een hoek altyd 90 grade. Pythagoras se Stelling is 'n wiskundige stelling wat van toepassing is op reghoekige driehoeke. Die stelling lui as volg:

In enige reghoekige driehoek is die kwadraat van die lengte van die skuinssy gelyk aan die som van die kwadrate van die lengtes van die reghoekige sye.

By 'n gelyksydige driehoek is al drie die sye ewe lank en al drie hoeke is altyd 60 grade. Die oppervlakte van so 'n driehoek met kante van lengte $L$ is gelyk aan ${\sqrt {3}}L^{2}/4$.

Vlak driehoek

'n Willekeurige driehoek

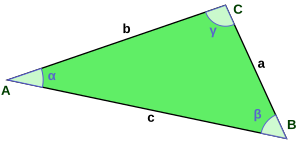
U moet trigonometrie gebruik om die verskeie waarde van 'n driehoek te bereken.

As u al drie lengte van al drie sye weet, kan jy die grote van die verskeie hoeke met die cosreël bereken:

$c^{2}=a^{2}+b^{2}-2ab\cos \gamma$

As die hoek $\gamma$ 90° is, is $\cos \gamma =0$ en die vergelyking ontaard na

$c^{2}=a^{2}+b^{2}$ (die wet van Pythagoras).

As u die waarde van twee sye en een hoek weet, kan jy die waarde van die derde sy en die ook die andere hoeke met die sinreël bereken:

${\frac {\sin \alpha }{a}}={\frac {\sin \beta }{b}}={\frac {\sin \gamma }{c}}$

U kan die oppervlak $A$ van 'n vlak driehoek met hierdie vergelyking bereken:

$A={\frac {1}{2}}ab\sin \gamma$

Sferiese driehoek

'n Sferiese driehoek

As die afstande voldoende groot is om die kromming van die aarde in ag te neem, moet u sferiese driehoeke gebruik eerder as gewone driehoeke om te navigeer.

(Let wel - al die hoeke in hierdie sferiese meetkunde formules is in in radiale aangedui).

Die reëls vir sferiese meetkunde veronderstel dat die radius van die bol 1 is, dus is die lengtes van die boë $a$, $b$ en $c$ gelyk aan die hoeke wat hulle in die middel van die bol trek. Die werklike lengtes van hierdie boë is $ar$, $br$ en $cr$ waar $r$ die radius van die sfeer is.

U kan die oppervlak $A$ van die sferiese driehoek met hierdie vergelyking bereken:

$A=(a+b+c-\pi )r^{2}$

Albei die sinreël en die cosreël dra oor van vlak driehoeke na sferiese driehoeke. Die sinreël is:

${\frac {\sin a}{\sin \alpha }}={\frac {\sin b}{sin\beta }}={\frac {\sin c}{\sin \gamma }}$

Die cosreël lui:

$\cos a=\cos b\cos c+\sin a\sin b\cos \alpha$

en

$\cos \alpha =-\cos \beta \cos \gamma +\sin \beta \sin \gamma \cos a$

Sien ook

• Tetraëder