Faraday se wet
Faraday (Michael Faraday) se wet van induksie bepaal dat 'n elektriese stroom wat verander met tyd 'n eweredige elektromotoriese krag veroorsaak.
Faraday se wet
[wysig | wysig bron]
Faraday se wet word gewoonlik uitgedruk as:
Vir 'n draadlus in 'n magneetveld word die magnetiese vloed gedefinieer vir enige oppervlak waarvan dié se grens die gegewe lus is. Aangesien die draadlus kan beweeg, skryf ons vir die oppervlak. Die magnetiese vloed is die oppervlakintegraal:
- waar 'n element van die oppervlakte van die bewegende oppervlak is
- die magneetveld is, en
- 'n vektorpuntproduk is wat die vloed deur voorstel.
In meer visuele terme is die magnetiese vloed deur die draadlus in direkte verhouding met die aantal magneetveldlyne wat deur die lus gaan.
In die geval van 'n spoel of induktor illustreer die volgende vergelyking die wet:
- waar V die elektromotoriese krag is,
- die magnetiese vloed deur een draadlus is,
- die tyd-veranderende tempo van die magnetiese vloed is, en
- N die aantal windings draad in die spoel is.
Die linkerhandreël
[wysig | wysig bron]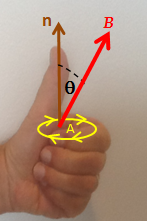
Die wette van induksie van elektriese strome in wiskundige vorm is in 1845 deur die Duitse fisikus Franz Ernst Neumann vasgestel[3] en die rigting van die elektromotoriese krag word deur Lenz se wet gegee. Faraday se wet bevat die inligting oor die verwantskappe tussen die groottes en die rigting van die veranderlikes daarvan. Die verhoudings tussen die aanwysings is egter nie eksplisiet nie; hulle word in die wiskundige formule versteek.
Dit is moontlik om die rigting van die elektromotoriese krag direk uit Faraday se wet uit te vind, sonder om Lenz se wet te gebruik. 'n Linkerhandreël help om dit te doen, soos volg:[4][5]
- Rig die geboë vingers van die linkerhand in lyn met die lus (geel lyn).
- Strek jou duim. Die gestrekte duim dui die rigting van n (bruin) aan, die normale tot die gebied wat deur die lus omsluit word.
- Vind die teken van , die verandering in vloed. Bepaal die aanvanklike en finale stroom (waarvan die verskil is) ten opsigte van die normale n, soos aangedui deur die gestrekte duim.
- As die verandering in vloed, , positief is, wys die geboë vingers in die rigting van die elektromotoriese krag (geel pylpunte).
- As negatief is, is die rigting van die elektromotoriese krag teenoor die rigting van die geboë vingers (teenoor die geel pylpunte).
Geskiedenis
[wysig | wysig bron]
Elektromagnetiese induksie is onafhanklik ontdek deur Michael Faraday in 1831 en Joseph Henry in 1832.[7] Faraday was die eerste wat die resultate van sy eksperimente gepubliseer het.[8][9]
In Faraday se eerste eksperimentele demonstrasie van elektromagnetiese induksie (29 Augustus 1831)[10] draai hy twee drade om die teenoorgestelde kante van 'n ysterring (torus) ('n rangskikking soortgelyk aan 'n moderne toroïdale transformator). Op grond van sy beoordeling van onlangs ontdekte eienskappe van elektromagnete, het hy verwag dat wanneer die stroom in een draad begin vloei, 'n soort golf deur die ring sou beweeg en 'n mate van elektriese effek aan die teenoorgestelde kant sou veroorsaak. Hy het die een draad in 'n galvanometer geprop en daarna gekyk terwyl hy die ander draad aan 'n battery gekoppel het. Hy het inderdaad 'n kortstondige stroom gesien (wat hy 'n "golf van elektrisiteit" genoem het) toe hy die draad aan die battery koppel, en 'n ander toe hy dit ontkoppel.[11] Hierdie induksie was te wyte aan die verandering in magnetiese vloed wat plaasgevind het toe die battery gekoppel en ontkoppel is.[6]
Binne twee maande het Faraday verskeie ander voorbeelde van elektromagnetiese induksie gevind. Hy het byvoorbeeld kortstondige strome gesien toe hy vinnig 'n staafmagneet in en uit 'n draadspoel skuif, en hy het 'n gelykstroom opgewek deur 'n koperskyf naby die staafmagneet te draai met 'n glybare elektriese leiding, wat die "Faraday se skyf" genoem is.[11]

Faraday het elektromagnetiese induksie verduidelik met behulp van 'n konsep wat hy "lyne van krag" genoem het. Wetenskaplikes het destyds egter sy teoretiese idees wyd verwerp, hoofsaaklik omdat dit nie wiskundig geformuleer is nie.[11] 'n Uitsondering was James Clerk Maxwell, wat in 1861-'62 Faraday se idees as basis van sy kwantitatiewe elektromagnetiese teorie gebruik het.[11][12][13]
In Maxwell se referate word die tydswisselende aspek van elektromagnetiese induksie uitgedruk as 'n differensiaalvergelyking wat die Engelse fisikus Oliver Heaviside "Faraday se wet" genoem het, alhoewel dit anders is as die oorspronklike weergawe van Faraday se wet, en beskryf nie bewegende elektromagnetiese krag nie. Heaviside se weergawe is die vorm wat vandag erken word in die groep vergelykings wat bekend staan as "Maxwell se vergelykings".
"Lenz se wet", geformuleer deur die Russiese fisikus Emil Lenz in 1834,[14] beskryf "vloed deur die stroombaan" en gee die rigting van die geïnduseerde elektromagnetiese krag en stroom as gevolg van elektromagnetiese induksie.
Verwyings
[wysig | wysig bron]- ↑ Jordan, Edward; Balmain, Keith G. (1968). Electromagnetic Waves and Radiating Systems (in Engels) (2de uitg.). Prentice-Hall. p. 100.
- ↑ Hayt, William (1989). Engineering Electromagnetics (in Engels) (5de uitg.). McGraw-Hill. p. 312. ISBN 0-07-027406-1.
- ↑ Neumann, Franz Ernst (1846). "Allgemeine Gesetze der inducirten elektrischen Ströme" (PDF). Annalen der Physik (in Duits). 143 (1): 31–44. Bibcode:1846AnP...143...31N. doi:10.1002/andp.18461430103. Geargiveer vanaf die oorspronklike (PDF) op 12 Maart 2020.
- ↑ Yehuda Salu (2014). "A Left Hand Rule for Faraday's Law". The Physics Teacher (in Engels). 52 (1): 48. Bibcode:2014PhTea..52...48S. doi:10.1119/1.4849156. Verduidelikingsvideo
- ↑ Salu, Yehuda. "Bypassing Lenz's Rule - A Left Hand Rule for Faraday's Law". www.PhysicsForArchitects.com (in Engels). Geargiveer vanaf die oorspronklike op 7 Mei 2020. Besoek op 15 Januarie 2021.
- ↑ 6,0 6,1 Giancoli, Douglas C. (2016). Physics: Principles with Applications, Global edition (in Engels) (5de uitg.). Pearson Education Limited. pp. 623–624. ISBN 978-1-292-06685-1.
- ↑ Errede, Steven (2007). "A Brief History of Electromagnetism" (PDF). Loomis Laboratory of Physics (in Engels). The University of Illinois, Urbana-Champaign. Besoek op 15 Januarie 2021.
- ↑ Ulaby, F.T.; Ravaioli, U. (2015). Fundamentals of Applied Electromagnetics (in Engels) (7de uitg.). Pearson Education. p. 255. ISBN 978-0-13-335698-4. Besoek op 15 Januarie 2021.
- ↑ "Joseph Henry". Member Directory, National Academy of Sciences (in Engels). Besoek op 15 Januarie 2021.
- ↑ Faraday, Michael; Day, P. (1 Februarie 1999). The philosopher's tree: a selection of Michael Faraday's writings (in Engels). CRC Press. p. 71. ISBN 978-0-7503-0570-9. Besoek op 15 Januarie 2021.
- ↑ 11,0 11,1 11,2 11,3 Williams, Leslie Pearce (1987). Michael Faraday. Da Capo series in science (in Engels). Da Capo Press. p. 531. Besoek op 15 Januarie 2021.
- ↑ Clerk Maxwell, James (1904). A Treatise on Electricity and Magnetism (in Engels). Vol. 2 (3de uitg.). Oxford University Press. pp. 178–179, 189.
- ↑ "Archives Biographies: Michael Faraday" (in Engels). The Institution of Engineering and Technology. Besoek op 15 Januarie 2021.
- ↑ Lenz, Emil (1834). "Ueber die Bestimmung der Richtung der durch elektodynamische Vertheilung erregten galvanischen Ströme [Oor die bepaling van die rigting van galvaniese strome wat opgewek word deur elektrodinamiese verspreiding]". Annalen der Physik und Chemie (in Duits). 107 (31): 483–494. Bibcode:1834AnP...107..483L. doi:10.1002/andp.18341073103.









