'n Keël met radius r , hoogte h en lengte van skuinssy l . 'n Keël is 'n driedimensionele geometriese vorm wat deur twee parameters beskryf word. Dit kan vergelyk word met die vorm van 'n (afgeslote) heksehoed.
Indien
r
{\displaystyle r}
h
{\displaystyle h}
l
{\displaystyle l}
Oppervlak kegel
=
π
l
r
=
π
r
(
r
2
+
h
2
)
{\displaystyle {\text{Oppervlak kegel}}=\pi lr=\pi r{\sqrt {(r^{2}+h^{2})}}}
Oppervlak basis
=
π
r
2
{\displaystyle {\text{Oppervlak basis}}=\pi r^{2}}
Totale oppervlak
=
π
l
r
+
π
r
2
=
π
r
(
r
+
(
r
2
+
h
2
)
)
{\displaystyle {\text{Totale oppervlak}}=\pi lr+\pi r^{2}=\pi r\left(r+{\sqrt {(r^{2}+h^{2})}}\,\right)}
Volume
=
1
3
π
r
2
h
{\displaystyle {\text{Volume}}={\frac {1}{3}}\pi r^{2}h}
Keël. Hier volg die oppervlak en volume van 'n keël .
Totale volume
Totale volume
=
1
3
π
R
2
H
{\displaystyle {\text{Totale volume}}={\frac {1}{3}}\pi R^{2}H}
Gedeeltelike volume
R
{\displaystyle R}
H
{\displaystyle H}
r
{\displaystyle r}
h
{\displaystyle h}
In terme van R, H en h:
Gedeeltelike volume
=
π
h
H
R
2
(
H
−
h
+
h
2
3
H
)
{\displaystyle {\text{Gedeeltelike volume}}=\pi {\frac {h}{H}}R^{2}\left(H-h+{\frac {h^{2}}{3H}}\right)}
In terme van R, H en r:
Gedeeltelike volume
=
1
3
π
R
2
H
(
1
−
r
3
R
3
)
{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi R^{2}H\left(1-{\frac {r^{3}}{R^{3}}}\right)}
In terme van R, r en h:
Gedeeltelike volume
=
1
3
π
R
3
h
R
−
r
(
1
−
r
3
R
3
)
{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi R^{3}{\frac {h}{R-r}}\left(1-{\frac {r^{3}}{R^{3}}}\right)}
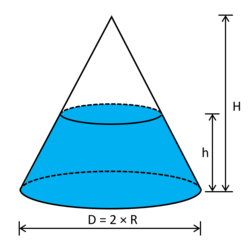
Gestel keël se dimensies is:
Kies 'n baie dun skyfie in die keël wat afstand h van die bopunt is met dikte dh.
Die radius van die dun skyfie, kan soos volg bepaal word:
r
R
=
h
H
{\displaystyle {\frac {r}{R}}={\frac {h}{H}}}
r
=
R
H
h
{\displaystyle r={\frac {R}{H}}h}
Die volume van die dun skyfie is die volgende:
d
V
=
π
r
2
d
h
=
π
(
R
H
h
)
2
d
h
=
π
(
R
H
)
2
h
2
d
h
{\displaystyle dV=\pi r^{2}dh\quad =\quad \pi \left({\frac {R}{H}}h\right)^{2}dh\quad =\quad \pi \left({\frac {R}{H}}\right)^{2}h^{2}dh}
Integreer nou van 0 tot H:
V
=
π
(
R
H
)
2
∫
0
H
h
2
d
h
{\displaystyle V=\pi \left({\frac {R}{H}}\right)^{2}\int _{0}^{H}h^{2}dh}
V
=
π
(
R
H
)
2
1
3
[
H
2
−
0
2
]
{\displaystyle V=\pi \left({\frac {R}{H}}\right)^{2}{\frac {1}{3}}\left[H^{2}-0^{2}\right]}
V
=
1
3
π
R
2
H
{\displaystyle V={\frac {1}{3}}\pi R^{2}H}
Gedeeltelike volume
=
1
3
π
R
2
H
−
1
3
π
r
2
(
H
−
h
)
{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi R^{2}H-{\frac {1}{3}}\pi r^{2}\left(H-h\right)}
=
1
3
π
[
R
2
H
−
r
2
(
H
−
h
)
]
{\displaystyle ={\frac {1}{3}}\pi \left[R^{2}H-r^{2}\left(H-h\right)\right]}
r
{\displaystyle r}
R
{\displaystyle R}
H
{\displaystyle H}
h
{\displaystyle h}
r
H
−
h
=
R
H
{\displaystyle {\frac {r}{H-h}}={\frac {R}{H}}}
r
=
R
H
(
H
−
h
)
{\displaystyle r={\frac {R}{H}}\left(H-h\right)}
Hierdie kan weer terug vervang word in die oorspronklike formule:
Gedeeltelike volume
=
1
3
π
[
R
2
H
−
R
2
H
2
(
H
−
h
)
3
]
{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi \left[R^{2}H-{\frac {R^{2}}{H^{2}}}\left(H-h\right)^{3}\right]}
(
H
−
h
)
3
=
H
3
−
3
H
2
h
+
3
H
h
2
−
h
3
{\displaystyle \left(H-h\right)^{3}=H^{3}-3H^{2}h+3Hh^{2}-h^{3}}
Vervang weer terug in hoof formule:
Gedeeltelike volume
=
1
3
π
R
2
[
H
−
1
H
2
(
H
3
−
3
H
2
h
+
3
H
h
2
−
h
3
)
]
{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi R^{2}\left[H-{\frac {1}{H^{2}}}\left(H^{3}-3H^{2}h+3Hh^{2}-h^{3}\right)\right]}
=
1
3
π
R
2
[
H
−
H
+
3
h
−
3
h
2
H
+
h
3
H
2
]
{\displaystyle ={\frac {1}{3}}\pi R^{2}\left[H-H+3h-3{\frac {h^{2}}{H}}+{\frac {h^{3}}{H^{2}}}\right]}
=
1
3
π
h
R
2
[
3
−
3
h
H
+
h
2
H
2
]
{\displaystyle ={\frac {1}{3}}\pi hR^{2}\left[3-3{\frac {h}{H}}+{\frac {h^{2}}{H^{2}}}\right]}
=
π
h
R
2
[
1
−
h
H
+
h
2
3
H
2
]
{\displaystyle =\pi hR^{2}\left[1-{\frac {h}{H}}+{\frac {h^{2}}{3H^{2}}}\right]}
=
π
h
H
R
2
[
H
−
h
+
h
2
3
H
]
{\displaystyle =\pi {\frac {h}{H}}R^{2}\left[H-h+{\frac {h^{2}}{3H}}\right]}
Gedeeltelike volume
=
groot kegel
−
klein kegel
{\displaystyle {\text{Gedeeltelike volume}}={\text{groot kegel}}-{\text{klein kegel}}}
Stel:
x
{\displaystyle x}
r
{\displaystyle r}
Gedeeltelike volume
=
1
3
π
R
2
H
−
1
3
π
r
2
x
{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi R^{2}H-{\frac {1}{3}}\pi r^{2}x}
Die verhouding tussen
x
{\displaystyle x}
r
{\displaystyle r}
H
{\displaystyle H}
R
{\displaystyle R}
x
r
=
H
R
⇒
x
=
r
H
R
{\displaystyle {\frac {x}{r}}={\frac {H}{R}}\qquad \Rightarrow \qquad x={\frac {rH}{R}}}
Dus:
Gedeeltelike volume
=
1
3
π
R
2
H
−
1
3
π
r
3
H
R
{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi R^{2}H-{\frac {1}{3}}\pi {\frac {r^{3}H}{R}}}
=
1
3
π
R
2
H
(
1
−
r
3
R
3
)
{\displaystyle ={\frac {1}{3}}\pi R^{2}H\left(1-{\frac {r^{3}}{R^{3}}}\right)}
Kry eers H in terme van R, r en h:
H
R
=
H
−
h
r
{\displaystyle {\frac {H}{R}}={\frac {H-h}{r}}}
H
R
=
H
r
−
h
r
{\displaystyle {\frac {H}{R}}={\frac {H}{r}}-{\frac {h}{r}}}
H
r
−
H
R
=
h
r
{\displaystyle {\frac {H}{r}}-{\frac {H}{R}}={\frac {h}{r}}}
H
(
1
r
−
1
R
)
=
h
r
{\displaystyle H\left({\frac {1}{r}}-{\frac {1}{R}}\right)={\frac {h}{r}}}
H
(
R
−
r
R
r
)
=
h
r
{\displaystyle H\left({\frac {R-r}{Rr}}\right)={\frac {h}{r}}}
H
=
R
r
h
r
(
R
−
r
)
{\displaystyle H={\frac {Rrh}{r\left(R-r\right)}}}
H
=
R
h
R
−
r
{\displaystyle H={\frac {Rh}{R-r}}}
Vervang hierdie nou in die formule wat in terme van R, H en r is:
Gedeeltelike volume
=
1
3
π
R
2
H
(
1
−
r
3
R
3
)
{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi R^{2}H\left(1-{\frac {r^{3}}{R^{3}}}\right)}
=
1
3
π
R
3
h
R
−
r
(
1
−
r
3
R
3
)
{\displaystyle ={\frac {1}{3}}\pi R^{3}{\frac {h}{R-r}}\left(1-{\frac {r^{3}}{R^{3}}}\right)}

 Wikiwoordeboek het 'n inskrywing vir keël.
Wikiwoordeboek het 'n inskrywing vir keël.

















![{\displaystyle V=\pi \left({\frac {R}{H}}\right)^{2}{\frac {1}{3}}\left[H^{2}-0^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e081b681b5df514a489da3b5f1b54c2b9e4d0fb4)


![{\displaystyle ={\frac {1}{3}}\pi \left[R^{2}H-r^{2}\left(H-h\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18a4d872d4fb1b7e28b2fdc9f68dacc96ece802c)


![{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi \left[R^{2}H-{\frac {R^{2}}{H^{2}}}\left(H-h\right)^{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bea65bc49e4f59efc89b646ca1337df73134f03)

![{\displaystyle {\text{Gedeeltelike volume}}={\frac {1}{3}}\pi R^{2}\left[H-{\frac {1}{H^{2}}}\left(H^{3}-3H^{2}h+3Hh^{2}-h^{3}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8606b80f95d20ddeb652cbf296f191adeeb07ba2)
![{\displaystyle ={\frac {1}{3}}\pi R^{2}\left[H-H+3h-3{\frac {h^{2}}{H}}+{\frac {h^{3}}{H^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95e8eb963f55e85338ad4365b9310d8c39c157c7)
![{\displaystyle ={\frac {1}{3}}\pi hR^{2}\left[3-3{\frac {h}{H}}+{\frac {h^{2}}{H^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc4433482ed423c6f4350c1f20d4202c50da6461)
![{\displaystyle =\pi hR^{2}\left[1-{\frac {h}{H}}+{\frac {h^{2}}{3H^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40d8781c3a421bb13c1bc28e6c6c0c3388ddc463)
![{\displaystyle =\pi {\frac {h}{H}}R^{2}\left[H-h+{\frac {h^{2}}{3H}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a823a98a51e835d0b21e3e1aea9edd415271e0)













