Platoniese vaste liggaam

Die vyf platoniese vaste liggame

'n Platoniese vaste liggaam is 'n konvekse vaste liggaam wat se oppervlak uit identiese reëlmatige veelhoeke bestaan. Daar is vyf sulke liggame – die tetraëder, heksaëder, oktaëder, dodekaëder en die ikosaëder. Hierdie liggame word al vanaf antieke tye bestudeer.

Wiskundige eienskappe

Die aantal vlakke, hoekpunte en sye van die vyf platoniese vaste liggame is gegee deur die Vergelyking van Euler:

$H+V=S+2$

waar

$H$ = aantal hoeke

$V$ = aantal vlakke

$S$ = aantal sye

Die aantal vir elke liggaam volg hieronder:

Platoniese vaste liggame
Naam	tetraëder	heksaëder	oktaëder	dodekaëder	ikosaëder
Puntgroep	Td	Oh	Oh	I	I
Vlakke	4	6	8	12	20
Vlaksoort	driehoek	vierkant	driehoek	vyfhoek	driehoek
Hoekpunte	4	8	6	20	12
Sye	6	12	12	30	30

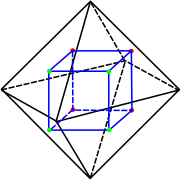
Elke platoniese liggaam het 'n duaalpoliëder Die duaal van enige liggaam is deur die aansluitings by die middelpunte van elke vlak met die middelpunte van ander vlakke gebou. Hieronder is dit bewys dat die duaal van die kubus die oktaëder is, en dat die duaal van die oktaëder die kubus is. Op dieselfde wyse is die duaal van die dodekaëder die ikosaëder en anders om. Die duaal van die tetraëder is die tetraëder self.

Kubus en oktaëder dualiteit

Die duaal van die oktaëder is die kubus. Die duaal van die oktaëder is die kubus.   Die duaal van die kubus is die oktaëder. Die duaal van die kubus is die oktaëder.

Platoniese liggame in die praktyk

Die driehoeke van 'n ikosaëder waarop die beskerming van die Maragheh sterrewag gebaseer is, is in rooi aangedui.

Raamwerke wat gebruik word om ander strukture te ondersteun, word dikwels gebaseer op een van die platoniese vaste stowwe. Kubusse is waarskynlik die meeste gebruik word, maar moderne argitektuur gebruik dikwels ander vorms. Een van die mees opvallende vorme wat deur platoniese liggame gebruik is, is dié van die geodesiese koepel.

Bron

• Cubdy, HM; Rollett, AR (1981). Mathematical Models (3de uitg.). Tarquin. ISBN 0 906212 20 0.