Topologie

Topologie, in wiskunde, van die Griekse τόπος (plek) en λόγος (studie) is die studie van die eienskappe van ruimte wat bewaar word onder voortdurende transformasie, bv. strek en buig, maar nie skeur of las nie. Dit kan bestudeer word deur die konsepsualisering van 'n versameling van deelversamelings, genaamd oop stelle, wat aan sekere eienskappe voldoen, wat vervorm kan word in wat bekend staan as 'n topologiese ruimte. Belangrike topologiese eienskappe sluit in koppelvlakke en kompaktheid.[1]
'n Voorbeeld van hierdie definisie is die topologiese ekwivalensie van 'n beker en 'n torus. (Sien regs)
Beginsels[wysig | wysig bron]
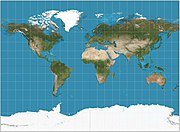
As 'n mens die Noordpool en die Suidpool ignoreer, is die twee wêreldkaarte hieronder, uit die oogpunt van 'n topoloog, identies.
| Twee topologies identies wêreldkaarte | |||||||||
| |||||||||
Elementêre topologie ondersoek die verhouding tussen rante, gesigte en hoeke. Twee voorbeelde van hierdie konsepte is die kubus en die Möbius strook. Die kubus, wat dikwels as 'n dobbelsteen gebruik word, het ses sye. Dit is ook eenvoudig om die aantal hoeke te tel (agt) asok die aantal rante (twaalf). Die Möbius strook is 'n interessante voorbeeld van topologie. Dit is in 1858 deur die Duitse wiskundige Möbius gekonsepsualiseer en het net een rant en net een gesig. Om dit te bewys, kan mens 'n streep op een kant van die strook trek sonder om dit om te draai, wanneer die pen terugkom tot die beginpunt loop die streep deur beide kante van die strook![2]
In 1756 het Euler die vergelyking vir 'n konvekse poliëder gepubliseer:
waar
- = hoekpunte (in Engels verticies)
- = kante (in Engels edges)
- = gesigte (in Engels faces)
Rante, hoeke en gesigte[wysig | wysig bron]
Een van die eerste probleme wat in topologie opgelos is, is die probleem van die sewe brûe in Königsberg: Is dit moontlik om elke brug net een keer in een uitstappie oor te steek? Hierdie probleem is deur Euler in 1736 opgelos.
| Sewe brûe in Königsberg | |||||||||
| |||||||||
In die topologiese voorstelling is die twee oewers en die twee eilande met blou punte verteenwoording. Die brûe is met swart strepe verteenwoordig. Met die hulp van hierdie voorstelling is dit maklik om te bewys dat die nie moontlik is om elke brug net eenmaal oorkruis sonder dat 'n mens sy voete nat kry.
Vierkleur kaart[wysig | wysig bron]
Die vierkleur stelling is vir die eerste deur Guthrie in 1852 voorgestel toe hy opgemerk het dat hy net vier kleure nodig het toe hy besig was om die graafskape van 'n kaart van Engeland in te kleur. Gedurende die 1960's en 1970's het Heinrich Heesch 'n rekenaar gebruik om die stelling te bewys. Hierdie stelling geld net vir 'n eenvoudige verbinde 2-dimensionele voorwerpe soos 'n stuk papier of die oppervlak van 'n 3-dimensionele voorwerp sonder gate. As daar 'n holte in die voorwerp is, is meer kleure nodig – byvoorbeeld is sewe kleure is nodig om enige patroon op 'n torus in te kleur.
| Vierkleur kaart | |||||||||
| |||||||||
Metropolitaanse spoorwegkaarte[wysig | wysig bron]
In baie stede ondergaan metropolitaanse spoorkaarte 'n topologiese verandering om dit makliker te maak om te volg. Hieronder volg voorbeelde van die Tyne and Wear Metro spoolyn:

Hierdie kaart toon al die krommes in die lyn en het ook 'n skaal wat die leser in staat stel om afstande te skat.

Op hierdie kaart is daar geen poging om afstande te wys nie, maar slegs die liggings van stasies relatief tot mekaar. Deels is die afstand tussen die stasies naby Monument versprei, om dit makliker te maak om die kaart te lees.
Verwysings[wysig | wysig bron]
- ↑ "Dictionary.com" (in Engels). 2016. Topology. Geargiveer vanaf die oorspronklike op 5 Maart 2016.
- ↑ (en) Gardiner, Martin (1985) [1977]. Mathematical Magic Show. Penguin Books. p. 123. ISBN 0-14-016556-8.